頑張る中3生へ
新年を迎え、高校入試が近づいてきました。香貫校の中3生も日々勉強に取り組んでいます。そんな中3生に今回は京都府の入試問題を用意しました。あまり解いたことのない問題かもしれませんが、決して難しいわけではないので、ぜひ解いてみてください。
【問題】
【問題】
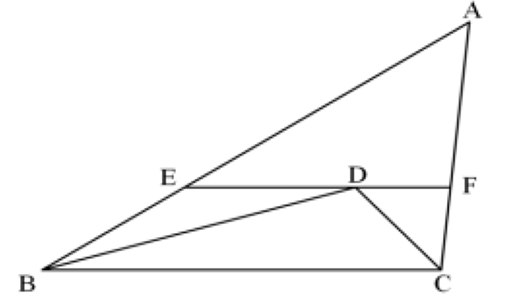
図のように△ABCがあり、AB=9cm、BC=7cmである。
∠ABCの二等分線と∠ACBの二等分線の交点をDとする。また点Dを通りBCに平行な直線とAB、ACとの交点をそれぞれE、Fとすると、BE=3cmであった。
このとき、線分AFの長さを求めなさい。
図のように△ABCがあり、AB=9cm、BC=7cmである。
∠ABCの二等分線と∠ACBの二等分線の交点をDとする。また点Dを通りBCに平行な直線とAB、ACとの交点をそれぞれE、Fとすると、BE=3cmであった。
このとき、線分AFの長さを求めなさい。
【解答・解説】
相似を利用してEFの長さを求める。
\begin{align}6:9=EF:7よりEF=\frac{14}{3}cm。\end{align}平行線の錯角より∠CBD=∠EDB、∠BCD=∠FDCなので△EBDと△FCDはそれぞれ二等辺三角形とわかるので、ED=3cm。 よって
\begin{align} FD=FC=\frac{14}{3}-3=\frac{5}{3}cmとなる。\end{align}AF=xとすると
\begin{align} x:\frac{5}{3}=2:1より、 x=\frac{10}{3}\end{align} \begin{align} 答え \frac{10}{3}cm\end{align}
最近はコロナやインフルエンザ等が流行っています。皆さんも体調管理には十分気を付けて、ラストスパート頑張っていきましょう。香貫校 宇田徳紀

